√ integration of 1/sec^2x tan^2x 289352

 1 Answer Tom ∫(1 tan2(x))sec2(x)dx We know 1 tan2(x) = 1 cos2(x) sec2(x) = 1 cos2(x) So we have ∫ 1 cos4(x) dx Let's t = tan(x) and dt = 1 cos2(x) dxIntegral of the form tan^m x sec^2x or cot^m x cosec^2x m is natural number Apne doubts clear karein ab Whatsapp par bhi Try it now CLICK HERE 1x 15x 2x Loading DoubtNut Solution for you Watch 1000 concepts & tricky questions explained! Ex 74, 9 sec 2 tan 2 4 Let tan = Diff both sides wrt x sec 2 = = sec 2 Integrating the function sec 2 tan 2 4 Putting value of tan = and = sec 2 = sec 2 t

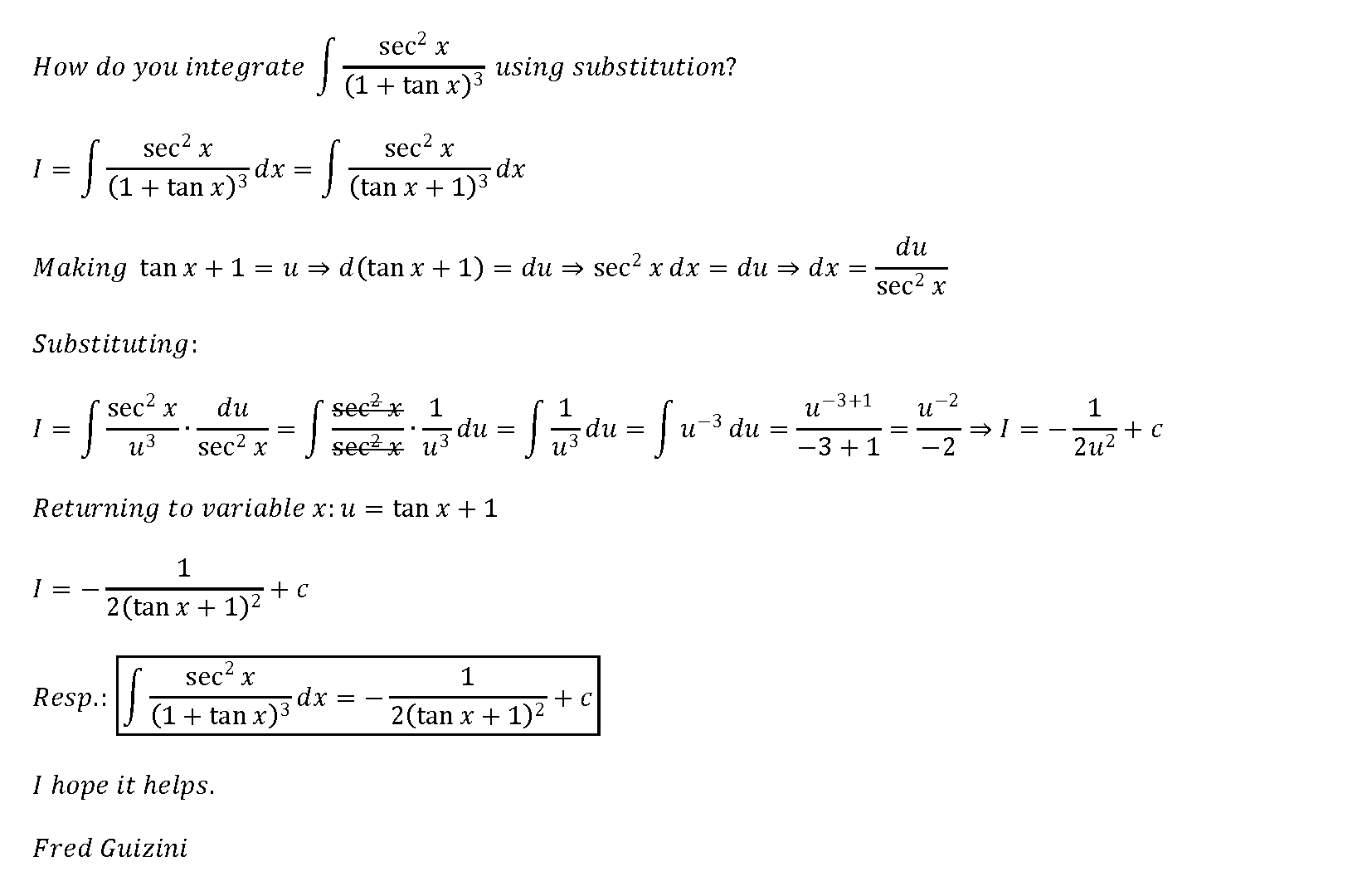
How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic

Integration of 1/sec^2x tan^2x

Integration of 1/sec^2x tan^2x-Learn integral of square of secant function with introduction and proof for integration of sec²(x) rule with respect to x to prove ∫sec²xdx = tanxcAnswer to Integrate the trigonometric integral integral of sec^2(x)/(1tan(x)) dx evaluated from 0 to pi/4 By signing up, you'll get thousands of

Integration Of Sec 2x 1 Tan 2x Maths

To integrate sec^22x, also written as ∫sec 2 2x dx, sec squared 2x, (sec2x)^2, and sec^2(2x), we start with a u substitution Let u = 2x This is a simple u substitution Therefore du/dx = 2 This is a simple differentiation step We rearrange the previous expression for dx We now have another integration on the RHS that means the same thing but is in terms of u We move the constant 1/2Sec 2 2x 1 Tan2x Youtube Integration of 1tan^2x/1tan^2x dx Integration of 1tan^2x/1tan^2x dx\\int \tan^{2}x\sec{x} \, dx\ > At last, the derivative of tan x 1/ sec x is one plus tan x upon sec x Y dash = (tanx1)dash sec x – (tanx1) sec x dash = sec^2x sec x (tanx1)sec x tan x Y dash = sec^3x – tan^2x sec x secx tanx Next, y dash = sec^2xtan^2x tanx/sec x = 1 tan x/sec x Derivative of tan x^ cot x Let y equals tan x to the power cot x The first

$$\int sec^2x \tan^2x dx = tan^2x 2\int \sec^2x \tan^2x dx$$ You can move the $ 2\int \sec^2x \tan^2x dx$ to the left hand side of the equation by addition $$\int \sec^2x \tan^2x dx 2\int \sec^2x \tan^2x dx= tan^2x c, c\in\mathbb{R}$$ Note that once we have a side without an integral on it you need to include a constant of integration ILearn how to solve trigonometric integrals problems step by step online Solve the trigonometric integral int(sec(2x)tan(2x))dx We can solve the integral \int\sec\left(2x\right)\tan\left(2x\right)dx by applying integration by substitution method (also called USubstitution) First, we must identify a section within the integral with a new variable (let's call it u), which when substitutedGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Integration of tan^2x sec^2x/ 1tan^6x dx Ask questions, doubts, problems and we will help you Integration of sec^2x integration of secant squared x Let try to solving, in this case we solve the \( \int(sec^2x) dx \) Once again, I = \( \int(sec^2x) dx \) Now multiply tanx/tanx with the sec^2x And we get, Assume that tanx = z Now differentiating on both side with respect to x sec 2 x dx = dz Hence, I = tanx c$$\int \sec^3(2x)dx = \frac{1}{2}\big(\tan(2x)\sec(2x) \ln \sec(2x)\tan(2x)\big) C$$ integration trigonometricintegrals Share Cite Follow edited Mar 6 '17 at 227 ziggurism 149k 2 2 gold badges 43 43 silver badges 97 97 bronze badges asked Mar 6 '17 at 215 user user 1,319 2 2 gold badges 11 11 silver badges 26 26 bronze badges $\endgroup$ 3

Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified

How Do You Find The Integral Of 1 Tan 2x Sec 2xdx Socratic

Click here👆to get an answer to your question ️ Prove that inttan x sec ^2x √(1 tan^2x)dx = 1/3 ( 1 tan ^2x )^3/2 Join / Login >> Class 12 >> Maths >> Integrals >> Integration by Substitution >> Prove that inttan x sec ^2 Question Prove that ∫ tan x sec 2 x 1 − tan 2 x d x = 3 1 (1 − tan 2 x) 3 / 2 Medium Open in App Solution Verified by Toppr Let I = ∫ tan x sec 2Follow Report by P6AGs7himoksh Log in to add a comment AnswersUsing substitution, u=tan (x) and du= sec^2 (x) dx U can integrate normally from there and substitute tan(x) back in, you'll get (1/3)tan^3 (x) c 1 reply Femto Badges 8 Rep?

View Question Prove The Equation Below Is An Identity

Solved 12 Evaluate The Integral Tan 2x 1 Sec 2x 1 Dx Chegg Com

Answer (1 of 5) Integration being the reverse process of differentiation, by observation is should be obvious that \tan{x} is what we are looking for But, let's do this a different way I = \int \sec^2{x}\;dx = \int \dfrac{\sec^2{x}\tan{x}}{\tan{x}} \;dx Let \sec{x} = t \implies dt = \sec{x}\Integral of sec^2 (x) \square!Integration of sec^2x/1tan^2x Close 7 Posted by 6 days ago Integration of sec^2x/1tan^2x youtube/_e6Mr2 0 comments share save hide report % Upvoted Log in or sign up to leave a comment log in sign up Sort by best

Integral Tan 2x Sec 2x 1 Tan 6x Dx Brainly In

Integration Trig Identities Ppt Download

Answer (1 of 3) I = sec 2xdx Multiplying in Nr and Dr by (sec 2xtan 2x ) I = {sec 2x(sec 2x tan 2x)/(sec 2x tan 2x)}dx Let (sec 2x tan 2x) = p then 2Click here👆to get an answer to your question ️ inttan^3 2x sec 2x dxIntegral of sec^2x \square!

Finding The Derivative Of Sec 2 X Video Lesson Transcript Study Com

How Many Can You Derive From First Principles Ppt Download

Integrate sec(2x)tan(2x) from 0 to We can solve the integral \int_{0}^{\frac{\pi}{6}}\sec\left(2x\right)\tan\left(2x\right)dx by applying integration by substitution method (also called USubstitution) First, we must identify a section within the integral with a new variable (let's call it u), which when substituted makes the integral easier We see that 2x it's aAnswer (1 of 10) \int \frac{1\tan^2x}{1\tan^2x} \,dx \int \frac{1\tan^2x}{\sec^2x} \,dx \int \frac{1\tan^2x}{\frac{1}{\cos^2x}} \,dx \int \cos^2x(1\tan^2x) \,dx Here, notice that sec^2x is already in the integral, and all that remains is tan^2x That is, we have tanx in squared form accompanied by its derivative, sec^2x This integral is ripe for substitution!

Int Dx Sec 2xtan 2x

What Is The Integral Of Sec X Sec 2x Quora

Integration of sec^2x/1tan x (Solution)Integration of sec^2x/1tan x (Solution) dx this video teaches us how to Integration of sec^2x/1tan x (Solution) dYes, sec 2 x−1=tan 2 x is an identity, sec 2 −1=tan 2 x, Let us derive the equation, We know the identity, sin 2 xcos 2 x=1 ——i Dividing throughout the equation by cos 2 x We get, sin 2 x/cos 2 x cos 2 x/cos 2 x = 1/cos 2 x We know that, sin 2 x/cos 2 x= tan 2 x, and cos 2 x/cos 2 x = 1, So the equation i after substituting becomes, tan 2 x 1= 1/cos 2 x ——–ii=sec^4(x)2sec^2(x)sec(x)tan(x)(1cos^2(x))/cos^4(x) =2sec^4(x)sec^2(x)2sec^2(x)sec(x)tan(x) The integrals of the second and third functions are standard!

10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com

Integral Of Sec 2x Tan 2x Integral Example Youtube

In the integral inttan^2xsec^2xdx, let u=tanx and du=sec^2xdx This gives us inttan^2xsec^2xdx=intu^2du Performing this integration yields u^3To integrate sec^4(x), there is a reduction formula, which I will post in a separate comment in a few minutes, but which must appear in calculus texts 74 views Share Related AnswerMath\begin{align} \displaystyle \int \frac{1 \tan^2(x)}{1 \tan^2(x)} \, \mathrm{d}x &= \displaystyle \int \frac{\left(\frac{\cos^2(x) \sin^2(x)}{\cos^2(x

Solved Evaluate The Following Integral Sec 2x Tan 2x Dx Sec Chegg Com

Integration Calculus Notes

 The last two answers, from Harish and egreg, are the same Integrating egreg's construction produces sec2x 2 C, and that from Harish produces tan2x 2 C1 Choosing C1 = 1 / 2 C for the latter, yields tan2x 1 2 C = sec2x 2 C, as itLearn how to solve definite integrals problems step by step online Integrate sec(2x)tan(2x) from 0 to We can solve the integral \int_{0}^{\frac{\pi}{6}}\sec\left(2x\right)\tan\left(2x\right)dx by applying integration by substitution method (also called USubstitution) First, we must identify a section within the integral with aThis video shows how to find the integral of sec(2x)*tan(2x)

Integration Tan Sec2x 1 Tan2x Dx Mathematics Topperlearning Com Fod22d

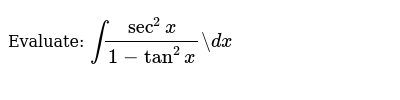
Evaluate Int Sec 2x 1 Tan 2x Dx

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Answer (1 of 3) \\displaystyle\\int \\dfrac{\\sec x}{\\tan^2 x}\\,dx =\\displaystyle\\int \\sec x\\cot^2 x\\,dx =\\displaystyle\\int \\csc x \\cot x\\,dx =\\csc x CNow, we can recognise sec^2 (x) as the derivative of tan (x) (you can prove this using the quotient rule and the identity sin^2 (x) cos^2 (x) = 1), while we get x when we integrate 1, so our final answer is tan (x) x c Answered by Warren L • Maths tutor

7 Techniques Of Integration Techniques Of Integration 7

Tan 2x Sec 2x 1 Sec 2x Tan 2x 1 10 12 2 Sarthaks Econnect Largest Online Education Community

 The derivative of tanx is 1 tan2x Then ∫tan2xdx = ∫ d dxtanxdx − x c = tanx − x c Share answered Mar 6 '19 at 1403 Gibbs Gibbs 7,029 4Answer to Evaluate the indefinite integral Integral of tan^3 (2x) sec(2x) dx By signing up, you'll get thousands of stepbystep solutions toYou can not integrate tan 2 x but you can integrate sec 2 x Since sec 2 x = 1 tan 2 x Then tan 2 x = sec 2 x1 so the intragral of tan 2 x dx = the integral of (sec 2 x1) dx = intrgral of sec 2 x dx integral of 1 dx = tanxx C Answered by Nandini P • Maths tutor 131 Views See similar Maths A Level tutors Need help with Maths?One to one online tuition can be a great way to

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Integral Of Secant Cubed Wikipedia

 `int tanx sec^2x sqrt(1tan^2x) dx` `int tanx sec^2x sqrt(1tan^2x) dx` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep The integral of the product of a constant and a function = the constant x integral of function Geometrical interpretation of indefinite integral Comparison between differentiation and integration By substitutionAnswer (1 of 2) I = \displaystyle \int \dfrac{\tan x \cdot \sec^2 x \cdot dx}{1 \tan^2 x} \text{Let } t = \tan x\implies dt = \sec^2 x \cdot dx \therefore IThe integral of sec^2(x)dx/tan^2(x) 3tan(x) 2 looks quite complicated, but it really isn't if we realise that sec^2(x) is simply the derivative of tan(

Solved Find The Indefinite Integral Use C For The Constant Chegg Com

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

So sec^2 (x)=1tan^2 (x) This is one of the three Pythagorean identities in trigonometry, but if you don't recognize it, try converting to sines and cosines 1/cos^2 (x)=1sin^2 (x)/cos^2 (x) Now, multiply each term by cos^2 (x) to get 1=cos^2 (x) sin^2 (x#10 Report 9 years ago #10 You are asked to evaluate Let Carry out this substitution and evaluate the resulting integral750 K views 517 K people like this Like Share Share Related Video

Differential Equation D 2 1 Y E X Sec 2 X Tan X Mathematics Stack Exchange

Solution Integral Of 3 Sec 2x 1 Tan 2x 1 Studypool

5 Hint Integrate by parts twice and in each case assume u to be the polynomial function and consider d v for the first integration by parts as d v = sec ⁡ ( x) ( sec ⁡ ( x) tan ⁡ ( x)) d x v = 1 2 secIntegrating \ (\int \tan^m x\sec^n x\dee {x}\) Subsection 1 Integrating ∫ tanm x secn xdx ∫ tan m ⁡ x sec n ⁡ x d x ¶ The strategy for dealing with these integrals is similar to the strategy that we used to evaluate integrals of the form ∫sinmxcosnxdx ∫ sin mClick here 👆 to get an answer to your question ️ Integration of tan^3(2x)sec2x 1 Log in Join now 1 Log in Join now Secondary School Math 8 points Integration of tan^3(2x)sec2x Ask for details ;

Tan 2x Formula What Is Tan 2x Formula Examples

What Is The Integration Of Tan 2x Solution Quora

Int Tan 2xsec 2x 1 Tan 6x Dx Youtube

Can I Integrate Math Tan 2 X Sec 3 X Math Using The Substitution Quora

Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12

Tan2x Sec2x ただの悪魔の画像

Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3

Integrate Sec 2x Method 1

Integral Of Secant Cubed Wikipedia

Integral 1 Tan 2 X Sec 2 X Youtube

Ex 7 6 24 Mcq Integrate E X Sec X 1 Tan X Dx Is A E X Cos X

Tan2x Sec2x ただの悪魔の画像

Integration Of

Integral Of Tan 2 X Sec X Youtube

Integration Of Trigonometric Functions

What Is The Integral Of Tanx Sec 2x 1 Tan 2x Quora

bestpictjcry Tan 2x Tan 2x

Sec 2 2x 1 Tan2x Youtube

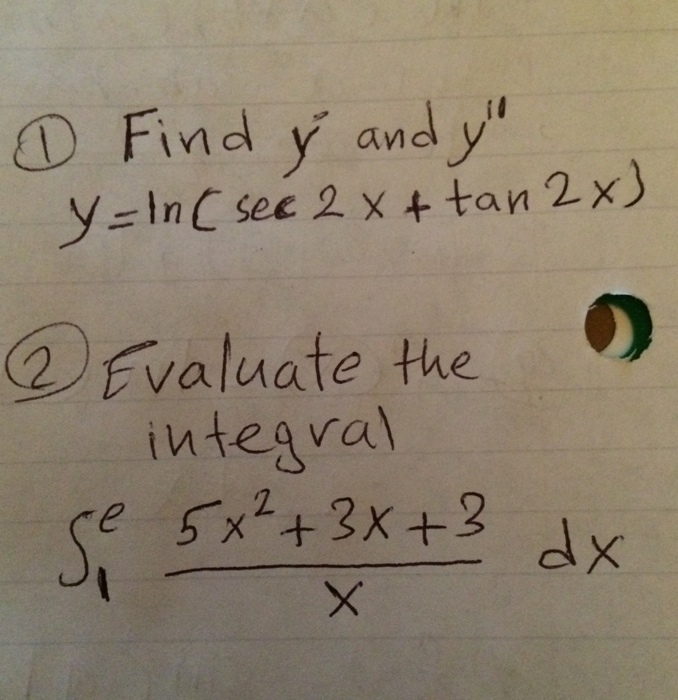
Solved 1 Find Y And Y Y Ln Sec 2x Tan 2x 2 Evaluate Chegg Com

Integrating Using Different Methods 60 Questions Teaching Resources

Get Answer 1 Tan2x Sec2x Dx Sin2x 2 C Tan 2 X 2 C 2sin X Cos X Transtutors

What Is Math Int Tan 2 2x Dx Math Quora

Integration Trig Identities Ppt Download

Ex 7 4 9 Integrate Sec 2 X Root Tan 2 X 4 Ncert Class 12

2

いろいろ Tan2x 1sec2x ただの悪魔の画像

Integration Of Sec 2x 1 Tan 2x Maths

Sec 1 1 Tan 2x 1 Tan 2 X

bestpictjcry Tan 2x Tan 2x

What Is The Integral Of Sec 2x Tan 2x Dx

Integration Tan Sec2x 1 Tan2x Dx Mathematics Topperlearning Com Fod22d

How Do You Integrate Int Sec 2x 1 Tanx 3 Using Substitution Socratic

Tan2x Sec2x ただの悪魔の画像

Evaluate Sec 2 X 16 Tan 2 X Dx Sarthaks Econnect Largest Online Education Community

The Integral Int Sec 2x Secx Tanx 9 2 Dx Equals For Some Arbitrary Constant K Dot 1 Secx Tanx 11 2 1 11 1 7 Secx Tanx 2 K 1 Secx Tanx 1 11 1 11 1 7 Secx Tanx 2 K 1 Secx Tanx 11 2 1 11 1 7 Secx Tanx 2 K 1

Q45 Integral Of 1 Tan 2x Sec 2x Youtube

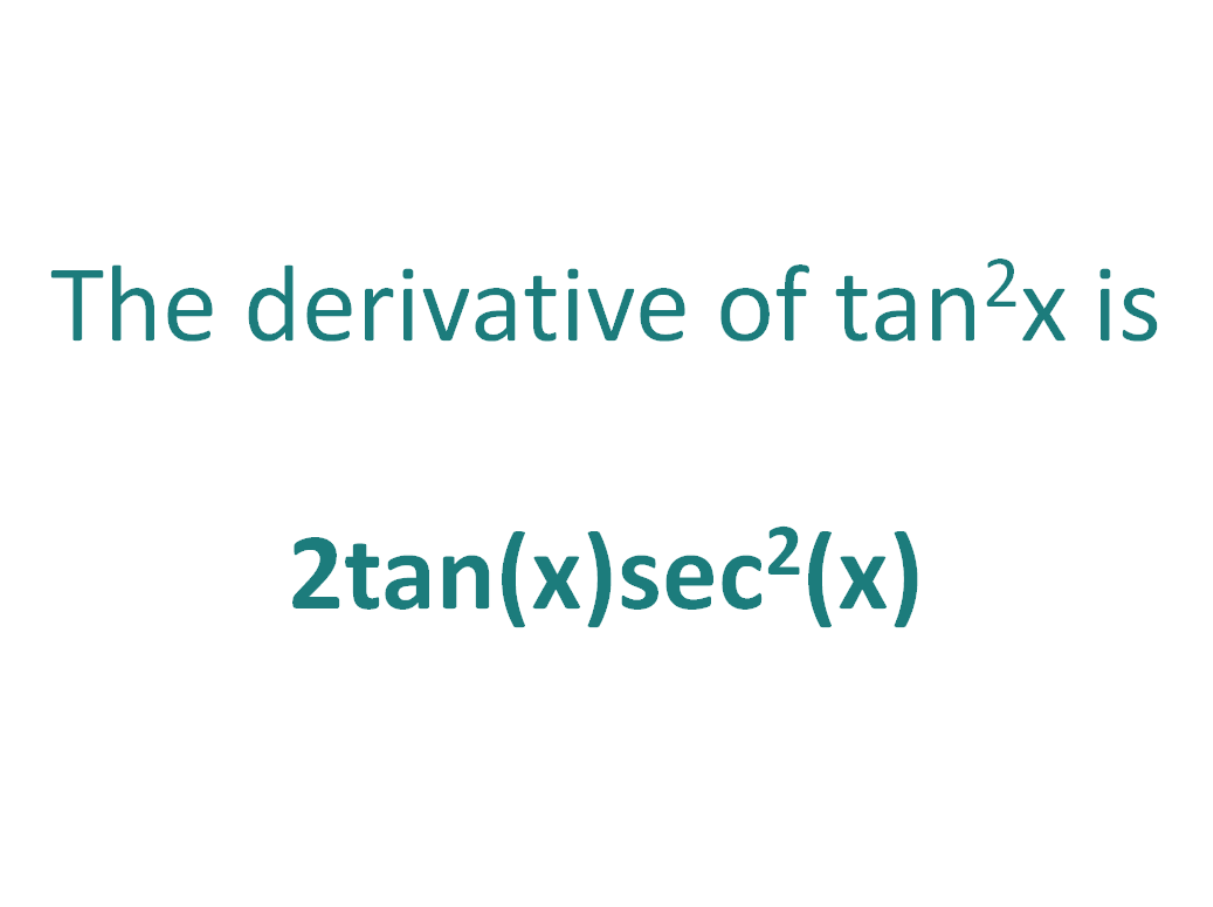
The Derivative Of Tan 2x Derivativeit

Trigonometric Identity With Pythagorens Sec 2x Sin 2x Cos 2x Tan 2x Youtube

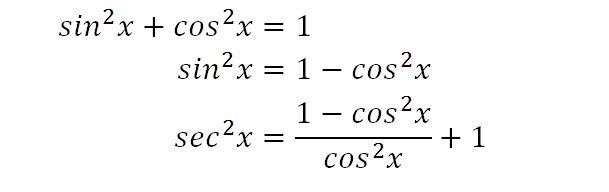
Integrate Sec 2x Method 2

Tan2x Sec2x ただの悪魔の画像

Solved Evaluate The Integral 34 Sec2x Tan 2x Dx 35 Chegg Com

Answered 3 1 Tanx Tan 2x Sec 2x S Bartleby

How Do We Prove That Tan2x 1 Sec2x Tanx Quora

いろいろ Tan2x 1sec2x ただの悪魔の画像

Integral Of Sec 2 X Sqrt 1 Tan 2 X Using The Arcsine Function Youtube

What Is Integral Of Sin2x Tan2x Quora

いろいろ Tan2x 1sec2x ただの悪魔の画像

Integral Sec2x Tan2x Dx Youtube

Integral Of Sec X Formula Proof Integration Of Sec X

Analytic Trig Ppt Video Online Download

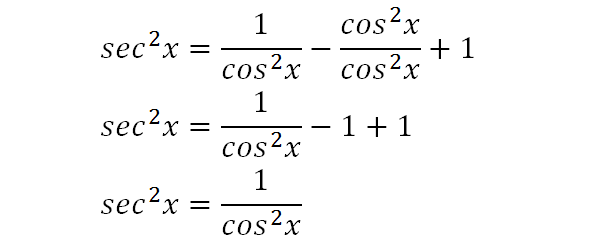
Integrate Sec 2x Method 2

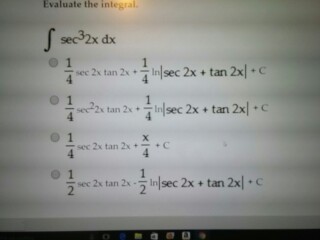
Solved Integral Sec 32x Dx 1 4 Sec 2x Tan 2x 1 4 In Sec Chegg Com

Bestmaths Online Proof 4

Integral Of Secant Cubed Wikipedia

Integration Of Tan 2 X Sec 2 X Youtube

Tan2x ただの悪魔の画像

Tan2x ただの悪魔の画像

Solved Question 1 Integrate The Following Function Sec 2x Chegg Com

1

What Is The Integral Of Tanx Sec 2x 1 Tan 2x Quora

Find Integral X 2 Sin 2 X Sec 2 X 1

Sec 2 2x 1 Tan2x Youtube

Integrate Sec 2x Method 2

How Do You Integrate 1 Tan2x Sec2x Dx Socratic

Solution Integrate This Function Sec 1 2x Tan 1 2x Dx

Math Problems Simplifying With Trigonometry Identities And Then Integration

3

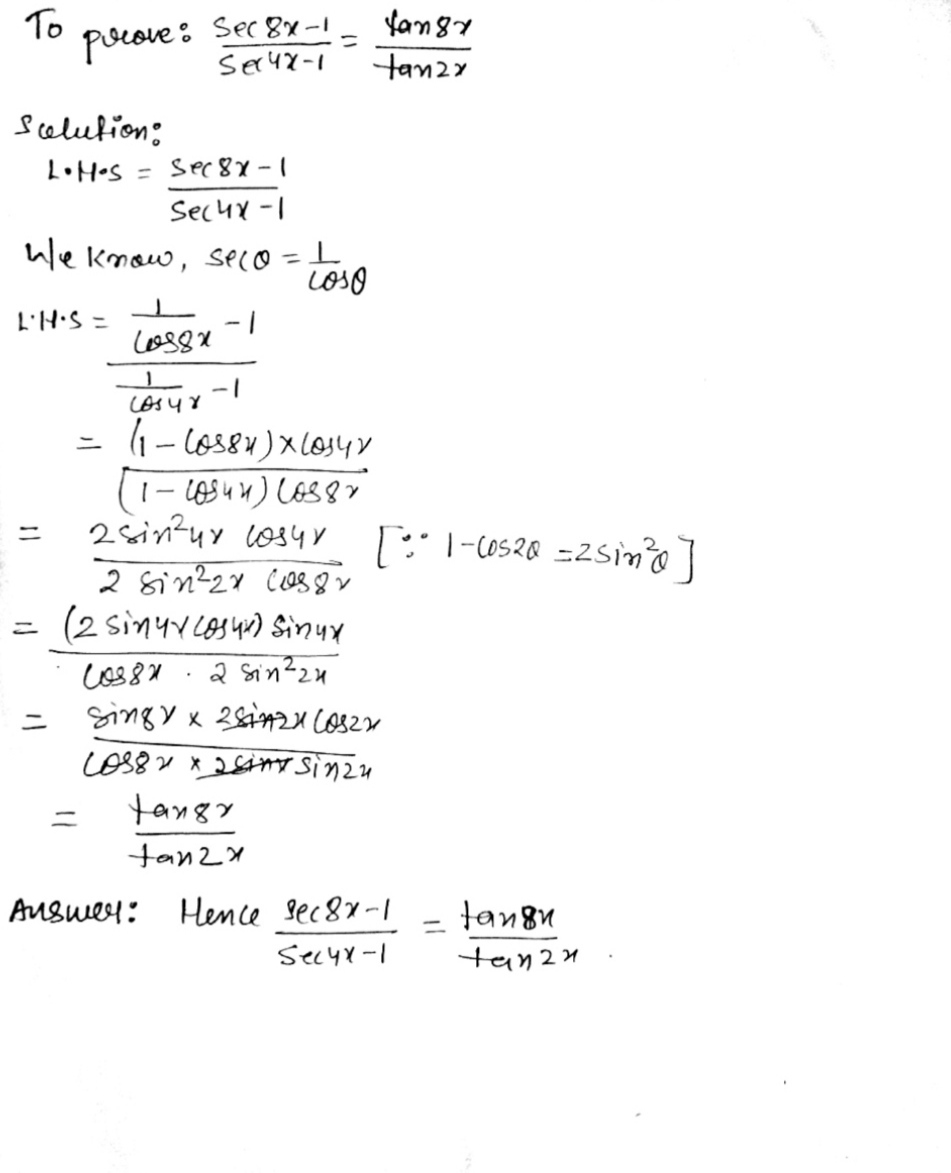
bestpictjcry Tan 2x Tan 2x

1

Finding The Derivative Of Sec 2 X Video Lesson Transcript Study Com

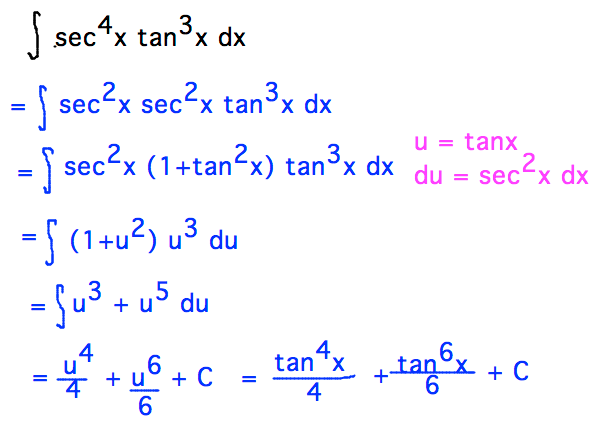
Geneseo Math 222 01 Trigonometric Integration

How Do You Integrate Int Sec 1 X Tan 1 X Dx Socratic

How Do You Evaluate The Integral 1 Tan X 3 Sec 2 X Dx Within The Range 0 Pi 4 Socratic

How To Integrate Math Tan 2 X Sec 6 X Math Using U Substitution Quora

bestpictjcry Tan 2x Tan 2x

Solution Integrate This Function Sec 1 2x Tan 1 2x Dx

Solved Evaluate Integral Tan 6 2x Sec 4 2x Dx If We Chegg Com

Ex 7 3 15 Integrate Tan3 2x Sec 2x Class 12 Ncert Ex 7 3

Find The Integrals Of The Functions Tan3 2x Sec 2x Mathematics Shaalaa Com

Solved Solve The Following Sec Order Non Homo Equation There Is Answer Provided Course Hero