[10000印刷√] 2tanx/1 tan^2x formula 273192

For instance, Sin 2X, Cos 2Y, Tan 2X, Sin 3X Thus, here we denote further various formulas for multiple angles Sin2X= 2SinX CosX= 2Tan X/1 Tan 2X;$\begingroup$ Well, if your instructor insisted that you do this by calling in the doubleangle formula, then I would replace my second paragraph with a criticism of the instructor for making things unnecessarily difficult Indeed, if the question had been to solve $\tan(9x/2)=1$, it would have been frustratingly difficult to use the ninefold angle formula and the halfangle formulas, i changed the tan2x into 2tanx/1tan^2 x then divided both sides by 2tanx but kinda ended up with tan^2 x=2 help P pLuvia Guest Use the double angle formula crap 3(2tanx)/(1tan^2x)=tanx Move the bottom thingo on the LHS to the RHSand u end up with something like this 6tanx=tanx (1tan^2x) u expand it

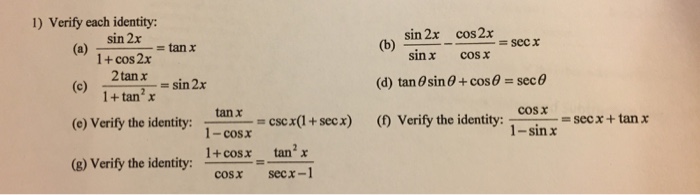
Solved Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com

2tanx/1 tan^2x formula

2tanx/1 tan^2x formula-Is not valid for x = 90°k180° and for tanx = ±1 so you have to test these values in the given equation The equation 3\tan^3 x \tan x = 0 factors as \tan x (\color {red} {3}\tan^2 x 1) = 0 (you forgot the 3) Hence, \tan x = 0 or \tan x = \pm \dfrac {1} {\sqrt {3}} Both of these should be easyTransformational Formula Here, we have two sets of transformational Formula

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

Solve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreBasic Trigonometric Function Formulas By using a rightangled triangle as a reference, the trigonometric functions and identities are derived sin θ = Opposite Side/Hypotenuse cos θ = Adjacent Side/Hypotenuse tan θ = Opposite Side/Adjacent Side sec θ = Hypotenuse/Adjacent Side Tan2x=2tanx/1tan^2x What is trigonometry formula?

 2tanx = 3 tan^2x tan^2x 2tanx 3 = 0 (tanx 3) (tanx 1) = 0 tanx = 3 or tanx = 1 if tanx = 3, x must be in II or IV by the CAST rule x = 1084° or 24° if x = 1, then x must be in I or III x = 45° or x = 225° 👍Tan2x=2tanx/1tan^2x Given this circumstance, what is the formula of trigonometry?Tan2x = 2tanx/(1tan 2 x) From this making tan 2 x the subject;

We will use the following trigonometric formula to prove the formula for tan 2x tan (a b) = (tan a tan b)/ (1 tan a tan b) We have tan 2x = tan (x x) = (tan x tan x)/ (1 tan x tan x) = 2 tan x/ (1 tan 2 x) Hence, we have derived the tan 2x formula using the angle sum formula of the tangent function1 tan^2x = sec^2x 1 Cot^2x = csc^2x tanx sinx/cosx cotx cosx/sinx Double Angle Formula see graph sin2x 2sinxcosx cos2x (1) cos^2xsin^2x cos2x (2) cos 2cos^21 cos2x (3) sin 1 sin^2x tan2x 2tanx/1tan^2x half angle formula see graphic The sign is determined by the quadrant in which the angle lies after being divided byTrigonometry Solve for x tan (2x)= (2tan (x))/ (1tan (x)^2) tan(2x) = 2tan(x) 1−tan2 (x) tan ( 2 x) = 2 tan ( x) 1 tan 2 ( x) Since x x is on the right side of the equation, switch the sides so it is on the left side of the equation 2tan(x) 1− tan2(x) = tan(2x) 2 tan ( x) 1 tan 2 ( x) = tan ( 2 x)

Solved Verify That Each Trigonometric Equation Is An Chegg Com

Tan 1 2tanx 1 Tan 2x Brainly In

Tan2x = 2tanx/(1tan^2x) How!Posted by Thrusha Keekan 4 years, 6 months ago CBSE > Class 12 > Mathematics 1 answers Pratit Luthra 4 years, 6 months ago sec 2 x=22tanx 1tan 2 x=22tanx tan 2 x2tanx1=0 (tanx1) 2 =0 tanx=1 Homework Statement cosx=12/13 3pi/2 is less than or equal to x is less than or equal to 2pi Homework Equations sin2x = 2sinxcosx cos2x = 12(sinx)^2 tan2x = (2tanx)/(1(tanx)^2) The Attempt at a Solution Using the tan2x formula, I get 60/47 Using

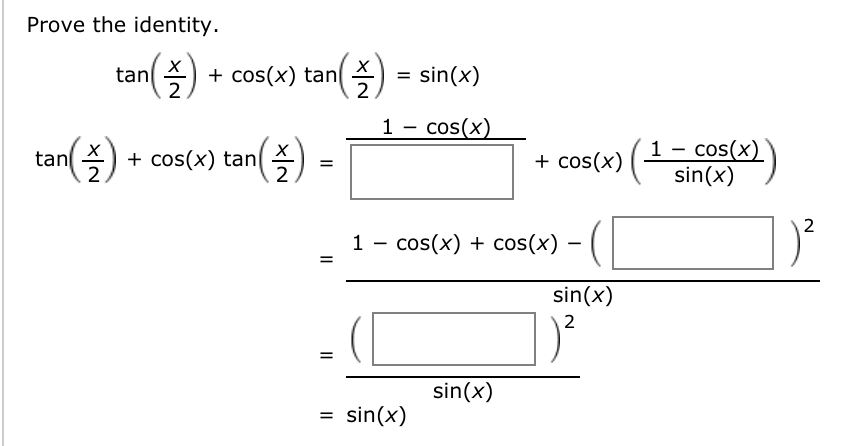
Solved Prove The Identity Cot 2x 1 Tan2x 2 Tan X Chegg Com

Integral 1 Tan 2 X Sec 2 X Youtube

 (It's a consequence of the Pythagorean theorem) There are other variants too, like tan²(x) 1 = sec²(x) when you divide both sides by cos²(x) Taking into account what is the formula for Tan2x? tan 2x = 2tanx/(1tan^2(x)) I actually should have used tformula But it is dragging me down when I write the one up here It is just a tedious work Just remember, when you substitue the tformula, always let t = tanx/2 (where x is the one that you are trying toFirst simply it by using tan2x formula Tan2x=2tanx/ (1tan^2 (x)) Then change it into sinx and Cosx In denominator you will get cos^2 (x)sin^2 (x) that is equal to cos (2x) In numerator you will get 2cos^2 (x) That is equal to 1cos2x It becomes (1cos2x)/cos2x =>sec2x 1 dsec2x /dx=2sec2xtan2x

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

Prove as an identity; if sinx=7/5 and angle x is in quadrant 2 and cos y=12/13 and angle y is in quadrant 1 find sin (xy) asked in TRIGONOMETRY by harvy0496 Apprentice doubleangleWe know that \(\tan (A B) = \frac{(tan A tan B)}{(1tan A tan B)}\) So tan (3x) can be considered as tan (x 2x) \(\tan (x 2x) = \frac{(tan x tan 2x)}{(1tan x tan 2x)}\) tan (2x) = tan (x x) \(\tan (x 2x) = \frac{(tan x tan (x x)}{(1 – tan x tan (x x)}\)\(\tan (x 2x) = \frac{tan x \frac{(tan x tan x)}{(1 – tan x tan x)}}{1 – tan x \frac{(tan x tan x)}{(1 – tan x tan x)}}\)\(\tan (x 2x) = \frac{tan x \frac{2tanx}{1 – tan^{2}x}}{1

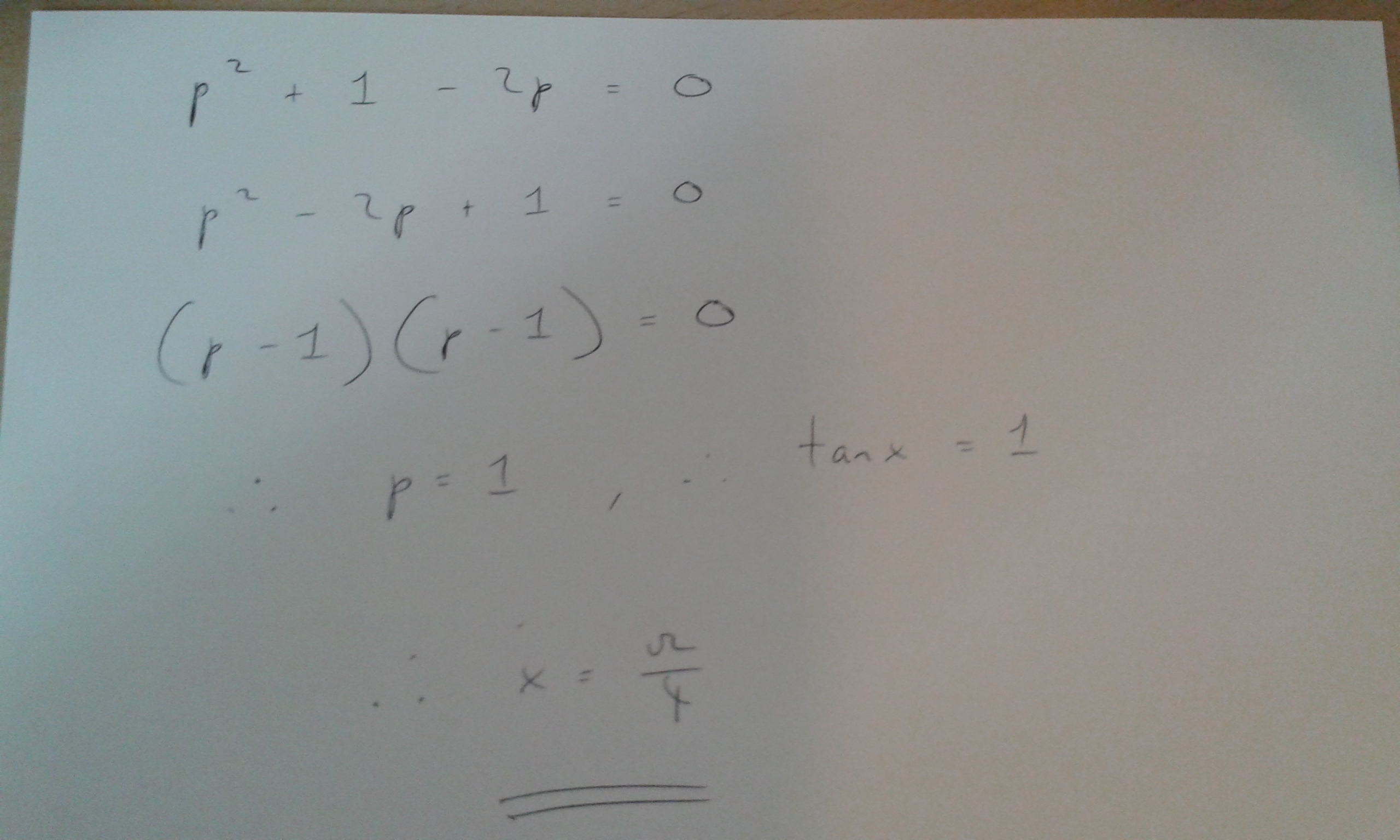
How Do You Solve Sec 2x 2tanx 0 Socratic

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

 Thanks in advance )tan2x = 2tanx / 1 tan^2x cotx= 1 / tanx Using these results you can simplify the equation to get 2 / 1 tan^2x = 3 3 tan^2x = 1 tan^2x = 1/ How to solve tan2xcotx3=0 Science Mathematics cos(2x) = 2cos 2 (x) − 1 = 2(04) 2 − 1 = −068 In the next exercise you are given information about an angle and asked to apply the double angle formulas to find the sine of the double angle and the cosine of the double angle Homework Statement ∫(1tanxtan(xa)dx Homework Equations The Attempt at a Solution ∫sec^xtan(xa) after that i don't know as i tried method of substitution by putting xa=t but i am not getting the answer as its form on the whole remains same

Prove That Tan2x 2tanx 1 Tan 2x Youtube

Solved Verify The Trigonometric Identities Sin 2x 2tanx 1 Tan 2 X Sin 3x 3sinx Cos 2 X Sin 3 X Use A Power Reducing Identity To Rewrite Th Course Hero

 The trigonometric identity `(tan^2x)/(1tan^2x) = sin^2x` has to be proved Start with the left hand side `(tan^2x)/(1tan^2x)` Substitute `tanx = sin x/cos x`Tan^2xtan^2y=sec^2xsec^2y and, how do you factor and simplify, cscx(sin^2xcos^2xtanx)/sinxcosx trig prove that the equation 2sin x cos x 4cos^2 x =1 may be written in the form of tan^2 x 2tan x 3=0 How do you verify theCos2X= Cos2X – Sin 2X = 1 2Sin2X= 2Cos2X1= 1Tan2 X/1 Tan2X;(1tan 2 x) tan2x = 2tanx 1 tan 2 x = 2tanx/tan2xtan 2 x = (2tanx/tan2x) 1 tan 2 x = 1 (2tanx/tan2x) substituting for tan 2 x in 2tan x tan2x 2a = 1 tan2x tan 2 x we have;

bestpictjcry Tan 2x Tan 2x

What Is The Formula Of Tan2x Quora

 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeThis is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Confirming that the result is an identity Yes, sec2−1=tan2x is an identityEl triángulo del ángulo doble se construye a partir de la tangente del ángulo doble tan2x = 2tanx 1 − tan 2x = cateto opuesto cateto adyacente A partir del triángulo del ángulo doble obtenemos las siguientes fórmulas • sen2x = 2tanx 1 tan 2x • cos2x = 1 − tan 2x 1 tan 2x • sec2x − 1 = tan2x tanx • sec2x 1

Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55

Sec 2 2x 1 Tan2x Youtube

Tan 2X = 2TanX/1 Tan2X;You can put this solution on YOUR website!Tan(2x) = sin(2x) cos(2x) Note These formulas are derived from the sum formulas in 54 using 2x= xx The formula for cos2xcan also be written as cos(2x) = cos2 x sin2 x = 2cos2 x 1 = 1 2sin2 x The formula for tan(2x) can be written as tan(2x) = 2tanx 1 tan2 x Example 1 Solve the following equations in the interval 0;2ˇ) (a)sin(2x) p 3cos

Is Tanx 2 2tanx 1 5tanx Sec X Quora

Ex 13 1 22 Lim X Pi 2 Tan 2x X Pi 2 Chapter 13 Class 11

 2 tanx 1 − tan2x = 2 sinx cosx 1 − ( sin2x cos2x) = 2sinx cosx cos2x −sin2x = sin2x cos2x = tan2x Proofs for sin2x = 2sinxcosx and cos2x = 1 −2sin2x Use Area of a ABC = 1/2 (base) (altitude) = 1/2 bc sin A Here, it is the ABC of a unit circle, with Tan2x tan 2×1x2 Sound that 2x upon 1 minus x square D is the differential operator int is the integration operator C is the constant of integration If x terminates in quadrant II then the point where the angle meets the unit circle is 512 Second formula in sin fornThe secant of x is 1 divided by the cosine of x sec x = 1 cos x , and the cosecant of x is defined to be 1 divided by the sine of x csc x = 1 sin x

Tan2x ただの悪魔の画像

Prove That Tan2x 2tanx 1 Tan 2x Youtube

Let's see tan(AB)= (tanAtanB)/(1tanA*tanB) Now putting B=A , we get, tan(AA)= (tanAtanA)/(1tanA*tanA) tan2A= 2tanA/(1tan^2A) Hope, now it's fine 2(sin x / cos x) / 1 – (sin²x / cos²x) = Now tan x = sin x / cos x (2 tan x) / 1 – (sin²x / cos²x) = Remember that tan²x = sin²x / cos²x (2 tan x) / (1 – tan²x) =RHS Hence Proved Alternative method LHS=tan{(2x)} =tan(xx) We know that tan (A B)= tan(A)tan(B) / 1 tan A tan B Applying the same formula we get =>tan(xx)= tan(x)tan(x) / 1 tan x tan x 2tan(x) / (1 –Sin(2x) = (2tan(x)) / (1tan^2(x)) *** Start with RHS 2tanx/(1tan^2x) 2tanx/(sec^2x) 2(sinx/cosx)/(1

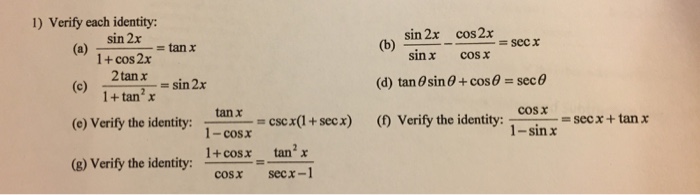
Solved Verify Each Identity A Sin 2x 1 Cos 2x Tan X Chegg Com

Proof For Tan 2x 2tanx 1 Tan X Trigonometry Youtube

Power reducing Identity sin^2 x sin^2 x = 1 cos (2x) / 2 power reducing Identity cos^2 x cos^2 x = 1 cos (2x) / 2 power reducing Identity tan^2 x 1 cos (2x) / 1 cos (2x) half angle formula for sine sin (x/2) = / square root of ( 1cosx ) / 2 half angle formula for cosineTan 2 ( x) = 1 3 tan 2 ( x) = 1 3 tan2(x) = 1 3 tan 2 ( x) = 1 3 Take the square square root of both sides of the equation equation to eliminate the exponent on the left side tan(x) = ±√1 3 tan ( x) = ± 1 3 The complete solution is the result of both the positive and negative portions of the solutionIn this video, we are going to learn how to derive the identity for sine of 2x in terms of tangent of x?sin(2x) = 2sin(x)cos(x)The proof of the identity has

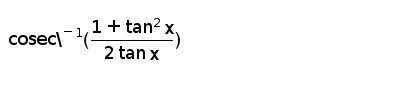
If 2tanx 1 Tan 2x 1 Then X Can Equal

Tangent Half Angle Formula Wikipedia

We know that, tan2x = (2tanx) / (1tan²x) Substituing the value of tan2x in (2), tan(2x x) = tanx {(2tanx) / (1tan²x)} / 1 {(2tanx) / (1tan²x)} tanx On solving, = (tanx tan 3 x 2tanx) / (1 tan 2 x 2tan 2 x) = (3tanx tan³x) / (1 3tan²x) Thus, tan3x =(3tanx tan³x) / (1 3tan²x) Hence, the formula of tan3x is (3tanx tan³x) / (1 3tan²x) The trigonometric equation is sec 2 (x) tan x = 2tan(x) tan x sec 2 (x) 2 = 0 ⇒tan x = 0 and sec 2 (x) 2 = 0 tan x = 0 tan x = tan 0 The genaral solution of tan(θ) = tan(α) is θ = nπ α, where n is an integer ⇒ x = nπ 0 x = nπn = 0,1,2 sec 2 (x) 2 = 0 sec 2 (x) = 2 Using reciprocal identity sec 2 x = 1/cosSolve equation for the exact solutions if possible put answer in degrees 2tanx/3tan^2x=1 calculus find sin2x, cos2x, and tan2x if sinx= 1/sqrt 5 and x terminates in quadrant II Tyler Find the solution {in the interval of 0,2pi)} of tan2x 2cosx = 0 ( I know the answer is pi/6, but I guessed and checked Please show the steps I need

1

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

 Tan2x=2tanx/1tan^2x What is Secx?Tan(x2x) = $\frac{tan(x)tan(2x)}{1 – tan(x)tan(2x)}$ Since $\frac{2 tanx}{1\tan 2x}$ Now, putting all the things together tan(3x) = tan(x) $\frac{2\tan ?(x)}{1\tan 2 x }$/1tan2(x) / 1 – tan(x) 2$(\frac{2tanx}{1\tan 2x})$ Multiplying the numerator and denominator by 1−tan (x) So, tan (3x) = $\frac{tan(x)tan3(x)2tan(x)}{1\tan 2(x)2tan2(x)}$ Hence, tanx= tan(2x) or tanxtan2x = 2 x= n pie 2x tanx2tanx/1tan 2 x=2 3x= n pie 2tan 2 x/1 tan 2 x=2 x= n pie/3 2tan 2 x=22tan 2 x 4 tan 2 x=2 tan 2 x= 1/2=tan 2 (tan 2 inverse 1/2) x= n pie tan inv (1/ root2) And youre done!!D

Math34 Trigonometric Formulas

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

 Is 1 tan 2x an identity?Cos (2x)= cos^2 (x) sin^2 (x) now tan 2x = sin 2x / (cos2x) now divide equations we got tan 2x= 2sinxcosx/ (cos^2 (x) sin^2 (x) Divids numerator and denominator by cos x Tan 2x=2tanc/ (1tan 2 (x)) level 2 deleted 1 point 2 years ago Higher 1tan^2x/1 tan^2x formula 1tan^2x/1 tan^2x formula2tan 2x = 1tan x fromwhich tan2 x =1 Takingthesquarerootthengives tanx =1 orView M2 Formuladocx from AMA 1110 at The Hong Kong Polytechnic University M2 Formula 2 Trigonometric 2 2 sin xcos x =1 1 sinx cosx= sin 2 x 2 2 sec x=1 tan x 2 2 cose c x=1cot x 1

If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2 Youtube

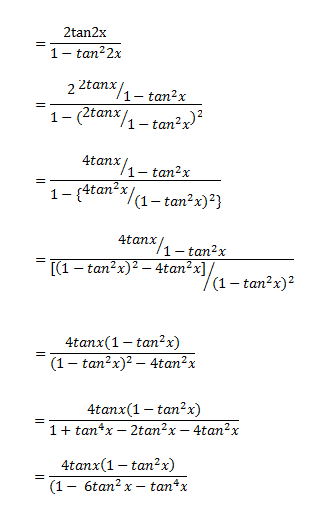
Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

Dear viewersIn this video, we will learn two formula proof for sin2x1) sin2x= 2sinxcosx2) sin2x = 2tanx/1tan²x#doubleangleformula#subscribe_plzif you waAnswer 2x Stepbystep explanation First you have to note that formula of tan(2x) So, tan(2x) = 2tan(x)/1tan^2(x) Now, tan1(2tanx/1tan^2x) = tan1(tan2x)Basic Trigonometric Function Formulas

Tinkutara Equation Editor Math Forum Question

Sin X 2 Tan X 2 1 Tan 2 X 2 Eraoco

 If f(2tanx/(1 tan2x)) = 1/2(1 cos2x)(sec2x 2tanx) then find f(x) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queriesThe double angle formula for tan2x is;

3

How Do You Solve Sec 2x 2tanx 0 Socratic

Solved Verify The Identity 1 Tan X 2 Sec 2 X 2 Tan X Chegg Com

If F 2tanx 1 Tan2x Then F 4 Youtube

Analytic Trig Ppt Video Online Download

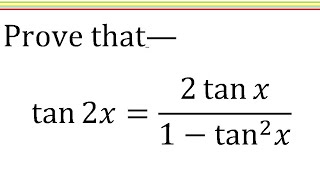
Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

Answered Verify The Identity 2 Tan X 1 Bartleby

What Is The Formula Of Tan2x Quora

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

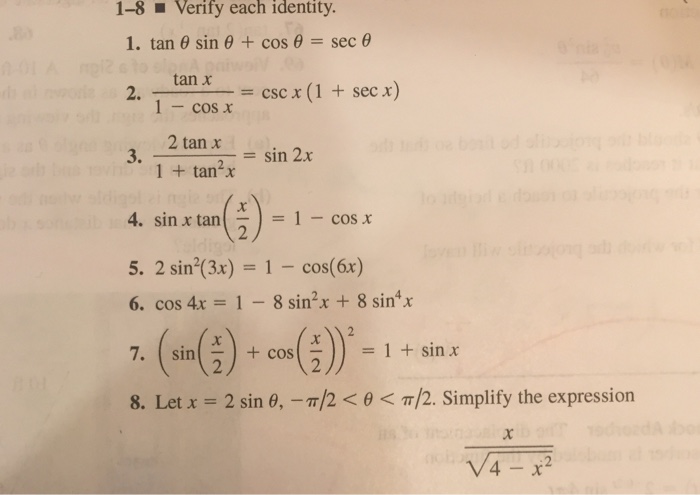
Solved 1 8 Verify Each Identity 1 Tan Sin Cos Sec Chegg Com

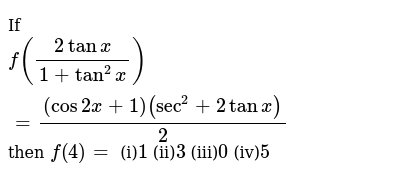
If F 2tanx 1 Tan 2 X Cos2x 1 Sec 2 2tanx 2 Then F 4 I 1 Ii 3 Iii 0 Iv 5

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Ex 3 3 23 Prove Tan 4x 4 Tan X 1 Tan2 X 1 6tan2x

Prove Sin2x 2tanx 1 Tan 2x Socratic

Tan2x 1 ただの悪魔の画像

Tan2x Tan 2x Identity For Tan2x Proof Of Tan2x Identity Formula For Tan2x Youtube

いろいろ Tan2x 1sec2x ただの悪魔の画像

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

Solved Verify The Trigonometric Identities Sin 2x 2tanx 1 Tan 2 X Sin 3x 3sinx Cos 2 X Sin 3 X Use A Power Reducing Identity To Rewrite Th Course Hero

Tan2x 2tanx 1 Tan X Trigonometric Identity Solve Hindi Youtube

In This Solution Why The 2 Tan2x 1 Tan 2x Was Dived By1 2tan 2x 1 Tan 2x 2 Trigonometric Functions Q23 Prove That Solution 4tanx La Tan X Maths Trigonometric Functions Meritnation Com

Solved Prove The Identity 1 Tan X 2 Tanx Csc 2x Note Chegg Com

How Do You Prove Tan 2x Secx 1 1 Secx Socratic

Bestpixtajpgjgh If F 2tanx 1 Tan 2x 1 Cos2x Sec 2x 2tanx 2 Then F 4

1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube

If F X 2tan X 1 Tan 2 X Then Value Of F Pi 4 Will Be

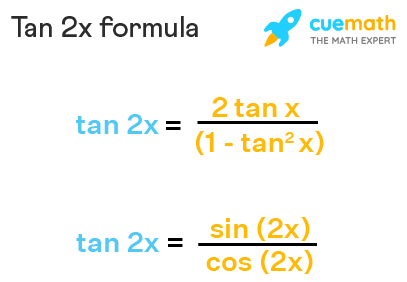
Tan 2x Formula What Is Tan 2x Formula Examples

Trig Identity Tan X 1 Tan 2 X Sec X Cos X Csc X Sin X Proved From Both Sides Youtube

1

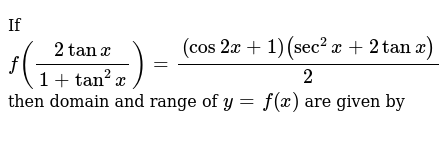
いろいろ Tan2x 1sec2x ただの悪魔の画像

Solved Verify The Identity 2 Tan X Sin 2x 1 Tan2 X 2 Chegg Com

How Do You Simplify The Identify Sin 2x 1 Cosx 1 Cosx Socratic

7 Proving Ids Trig Functions Identities

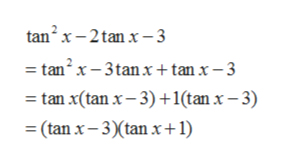
Answered Tan 2x 2tanx 3 Tanx 1 Bartleby

If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

What Is The General Solution Of X For Tan X Tan2x 1 Quora

Math34 Trigonometric Formulas

Prove That Tan2x 2tanx 1 Tan X Brainly In

Solved Verify That Each Of The Following Is An Identity Chegg Com

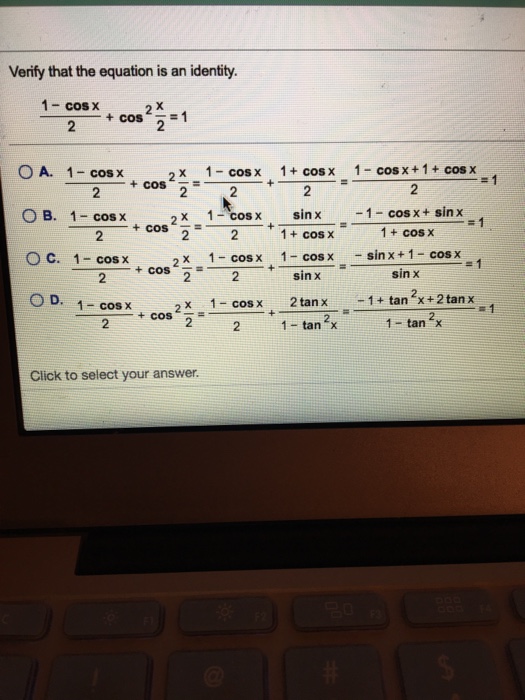
Solved Verify That The Equation Is An Identity 1 Cos X 2 Chegg Com

Trigonometry Identity Tan 2 X 1 Sec 2 X Youtube

Limit Trigonometric Function 2 Sec 2x 1 Tan X Youtube

2tanx Cos 2x Tanx 0 Solve Trig Equation Youtube

Ex 3 4 8 Find General Solution Of Sec 2 2x 1 Tan 2x Teachoo

Prove That Sin 2x Squared 2tanx Upon 1 Tan Square X Brainly In

How To Prove That Lhs Rhs Sin2x 2tanx 1 Tan Square X Quora

Is Tanx 2 2tanx 1 5tanx Sec X Quora

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

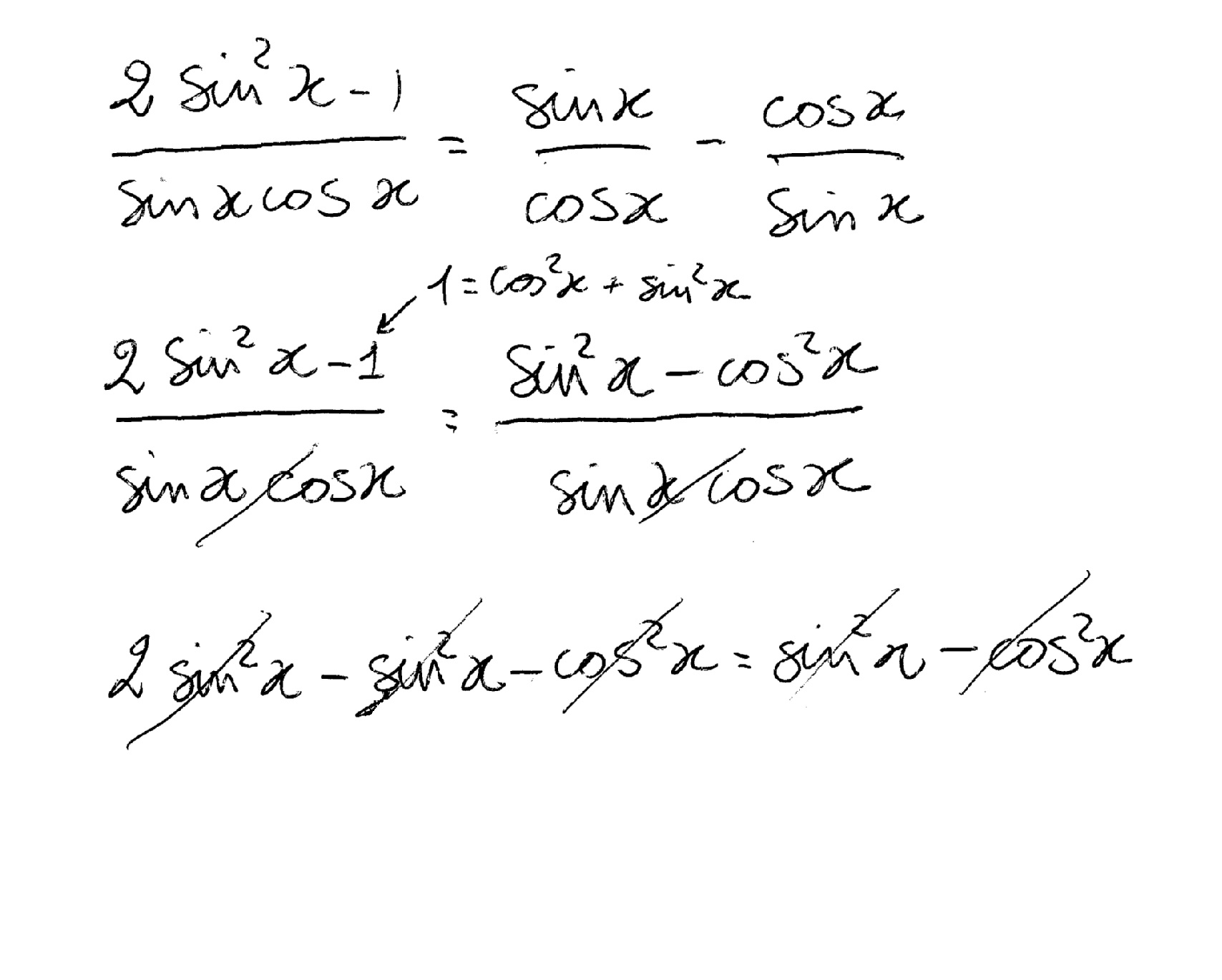
How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic

2tanx 1 Tan 2x 6181 2tanx 1 Tan 2x Formula

What Is The Formula Of Tan2x Quora

Tan2x ただの悪魔の画像

If F 2tanx 1 Tan 2x Cos2x 1 Sec 2x Tanx 2 Then F X

Chapter 7 Trigonometric Identities And Equations Ppt Download

If X 30 Verify That I Tan2x 2tanx 1 Tan 2x Ii Sinx Sqrt 1 Cos2x 2

Tan2x

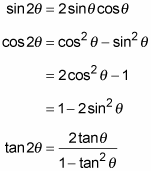
How Do You Prove That Cot2x Tan 2x 1 2tanx Socratic

Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3

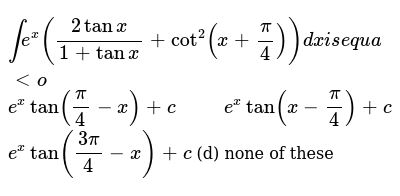
Inte X 2tanx 1 Tanx Cot 2 X Pi 4 Dxi Se Q U A Lto E Xtan Pi 4 X C E Xtan X Pi 4 C E Xtan 3pi 4 X C D None Of These

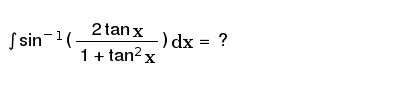
If 2tanx 1 Tan 2x 1 Then X Can Equal

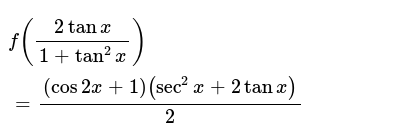
F 2tanx 1 Tan 2x Cos2x 1 Sec 2x 2tanx 2

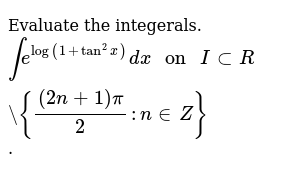
Evaluate The Integerals Br Int E Log 1 Tan 2 X Dx

Solved Prove Each Of The Following Identities Use The Sum Chegg Com

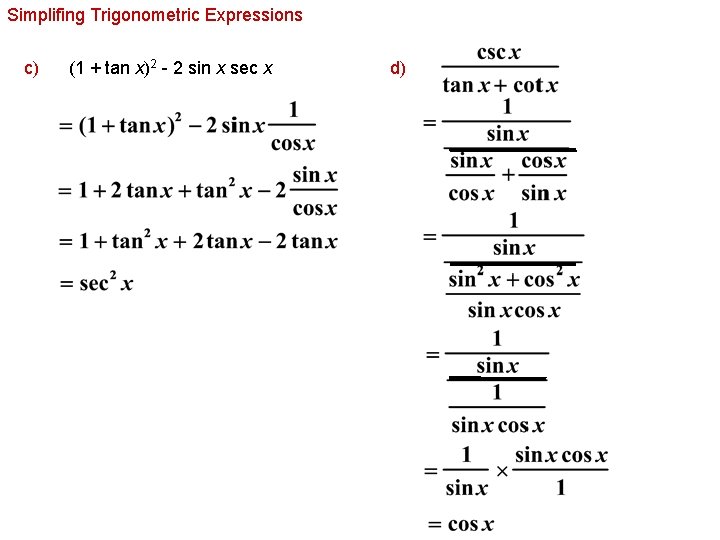
While You Wait Trigonometric Identities And Equations Section

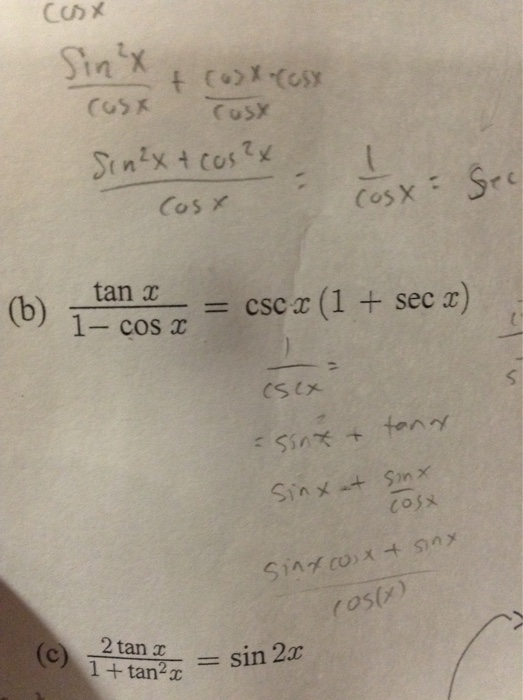
Solved B Tanx 1 Cosx Cscx 1 Secx C 2tanx 1 Tan 2x Chegg Com

Solved Let Tan 2x 1 2tan 2 Y Then Prove That Cos 2y 1 2cos 2x

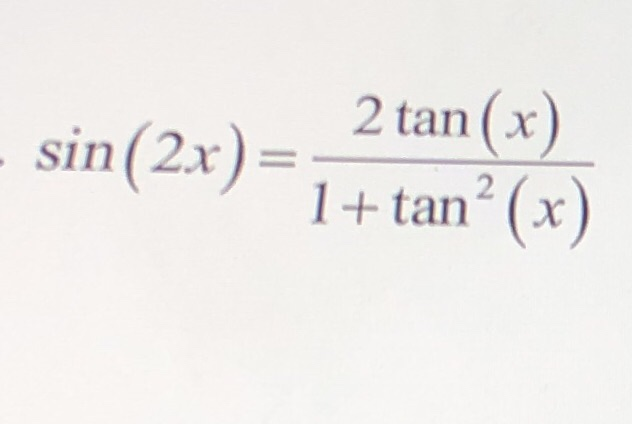
Solved Sin 2x 2tan X 1 Tan 2 X Sin 2x Chegg Com

What Is The Formula Of Tan2x Quora

Which Of The Following Are Solutions To 2tanx 1 Tan 2x Sqrt 3

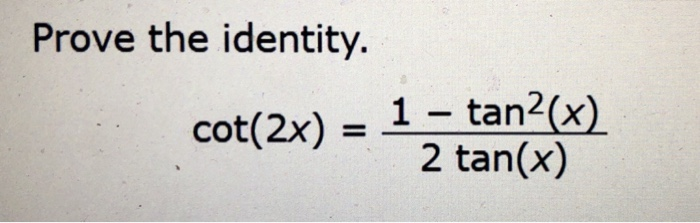
Solved Prove The Identity Cot 2x 1 Tan2 X 2 Tan X Chegg Com

Old Version Trig Show Sin 2x 2 Sin X Cos X 2tan X 1 Tan 2 X Youtube

Tan 2x Formula What Is Tan 2x Formula Examples